Temperature Control System – Design, Coding, PID Autotuning, and Lab Experiments
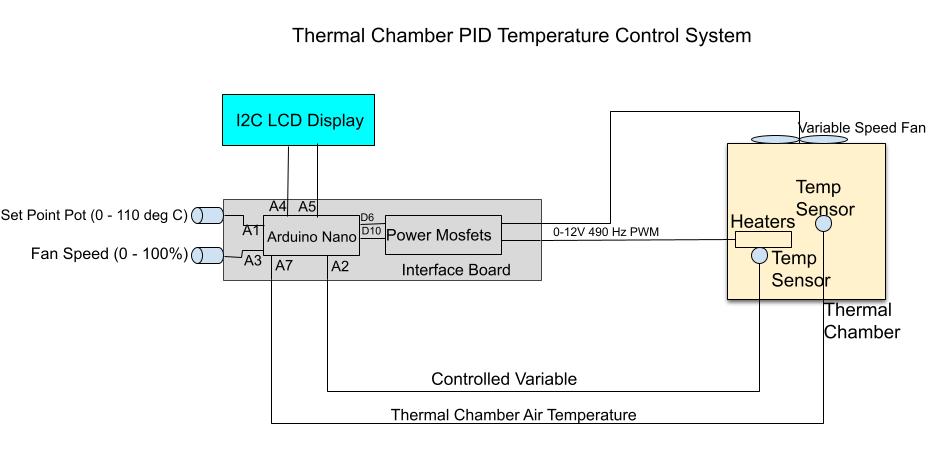
The block diagram above outlines the components of the Temperature control system for the thermal chamber. Photos of the actual components are shown below the block diagram. One sensor is contained between the 2 cement resistor heaters and attached to them so that response will be rapid and steady state temperature high. A 2nd sensor is located away from the heater elements in the center of the chamber. The response will be much slower and result in a much lower steady temperature than that of the sensor attached to and in between the heater elements.
A variable speed fan secured to the top of the chamber provides cooling which acts as the disturbance variable.
The schematic below shows the interconnection of the various components for the system
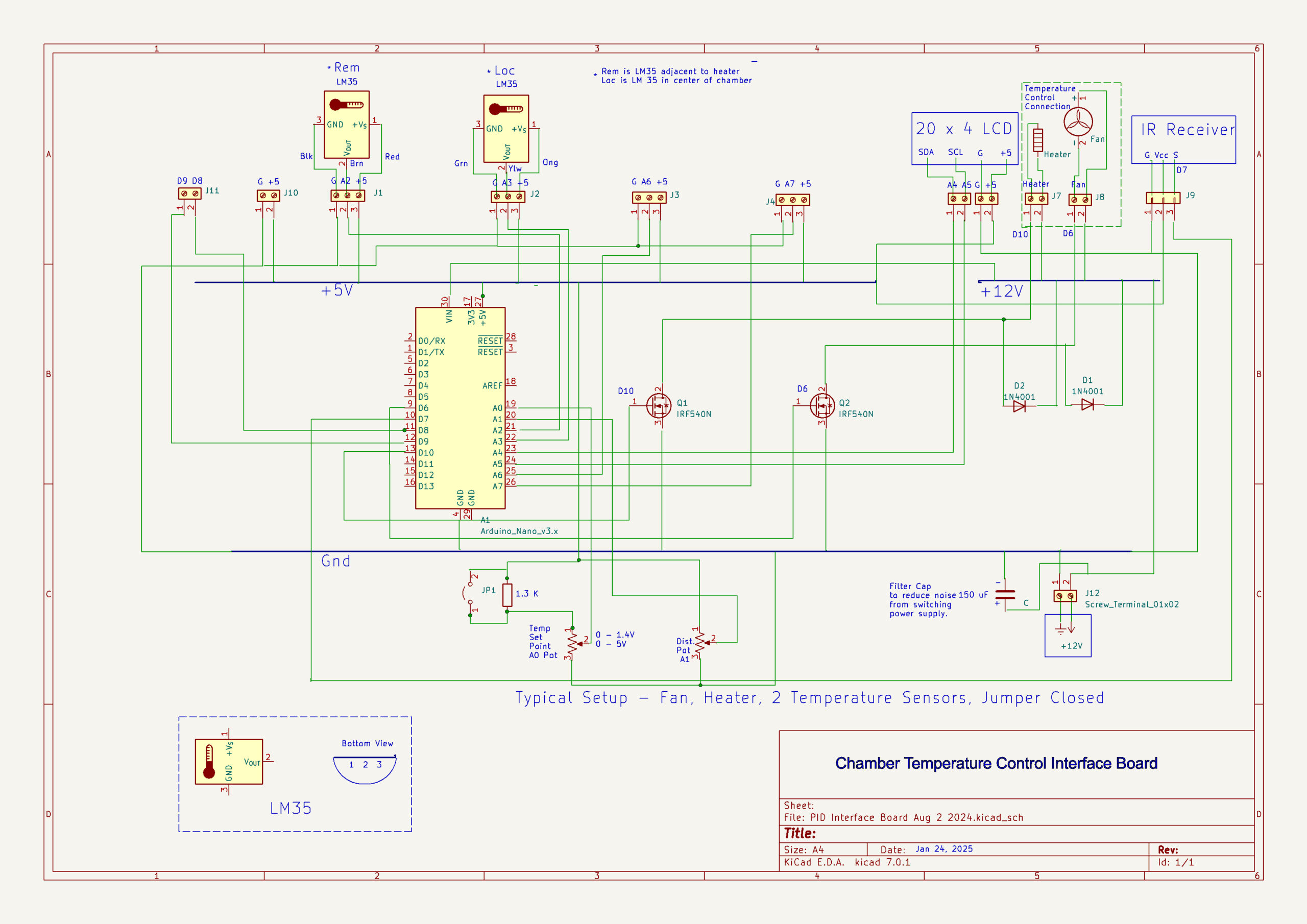
The interface uses a protyping board manufactured by PTSolns


The 2 photos below show the thermal chamber closed as well as open.
Two sets of terminals allow heating using either Heater 1 or Heater 2 as the heat source, or using both.

The 2 cement resistors are 36 ohms. The temperature sensors are LM35s and sense about 0 to 140 deg C. While not visible in the photo, one of the LM35s is secured in between the 2 cement resistor heating elements. It makes contact with both heating elements and thus measures the surface temperature of the element. The second LM35 is located away from the heating elements and measures the air temeperature of the sensors. Either LM35 can be selected as the controlled variable.
Small holes are situated at the front of the chamber to allow air flow through the chamber.

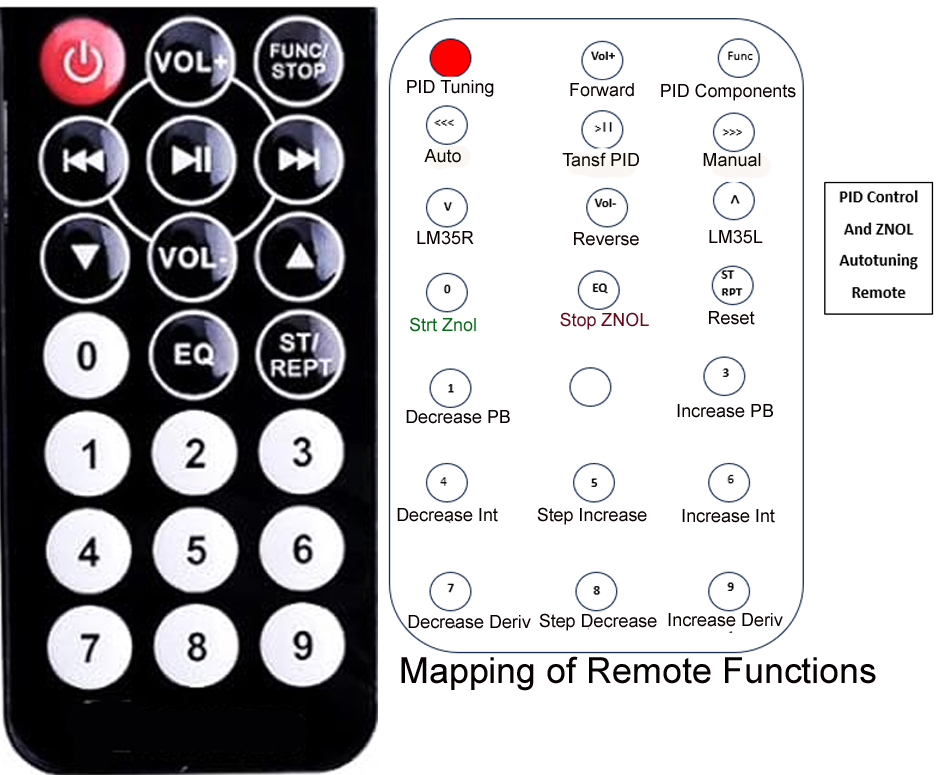
Operation of the Temperature Control System is done through an infra red remote. On the interface board, a potentiometer is used for either the Set Point when in Auto mode or a fixed heater setting when in Manual mode.
The control system has an Auto Tune feature for generating the Ziegler Nichols Quarter Decay tuning constants and automatically loading them into the PID controller.
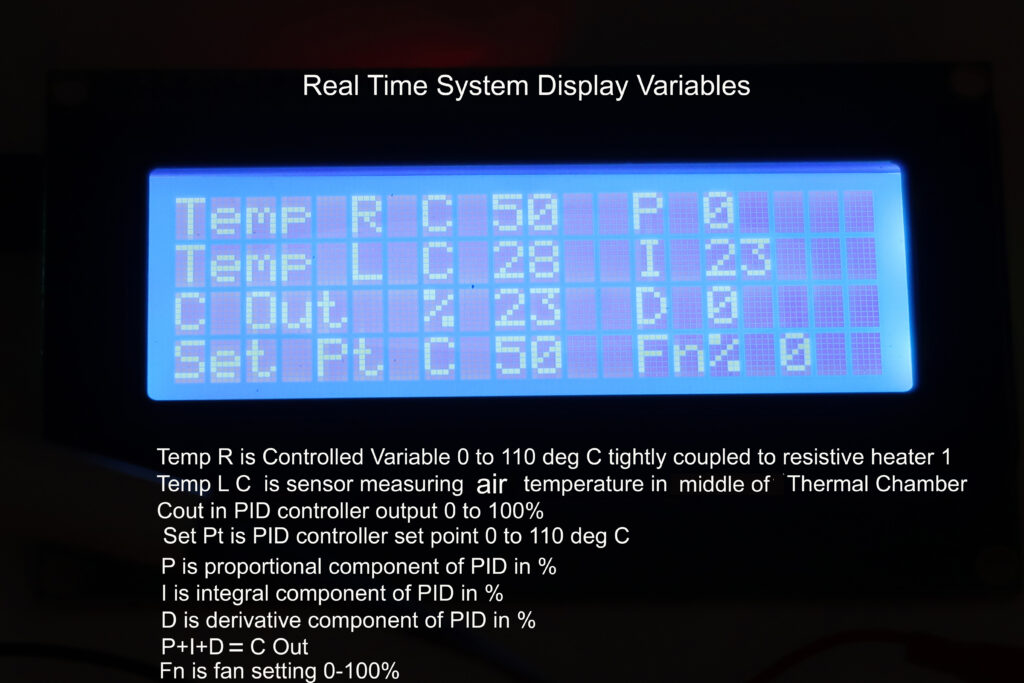
Display and monitoring is done using an LCD display and/or the plotting feature of the Arduino IDE.
The LCD displays process and control information. A valuable feature displays the proportional, integral, and derivative components that make up the controller output. When viewing the plotted variables on the Arduino IDE, the effects of each of the PID components yield insight into their interaction.
Code and Code Related

The following link is to the completeC/C++ code implemented using the Arduino IDE.
Complete Temperature Control C/C++ Code
The Following Link is to the PID Controller Function that is part of the Complete Temperature Control C/C++ Code
Function Declaration
float PID_output(float process, float setpoint, float Prop, float Integ, float deriv, int Interval, bool action)
Function Call
contOutNorm=PID_output(C_Variable/500, heaterSetting/500,propBand, integralTime, derivativeTime, 1000, controlAction);
The C_Variable which is the filtered temperature sensor, and the heaterSetting which is the Set Point generated by the Set Point potentiometer are normalized 0.0 to 1.0 by dividing the 2 variables by 500, the full temerature range corresponding to maximum voltage at the analog input to the Nano microcontroller. The LM35 sensor will only generate a voltage of 0 to 1.4 Volts corrsponding to 0 to 140 deg C, but the analog input is 0 to 5V which corresponds to 0 to 500 deg C.
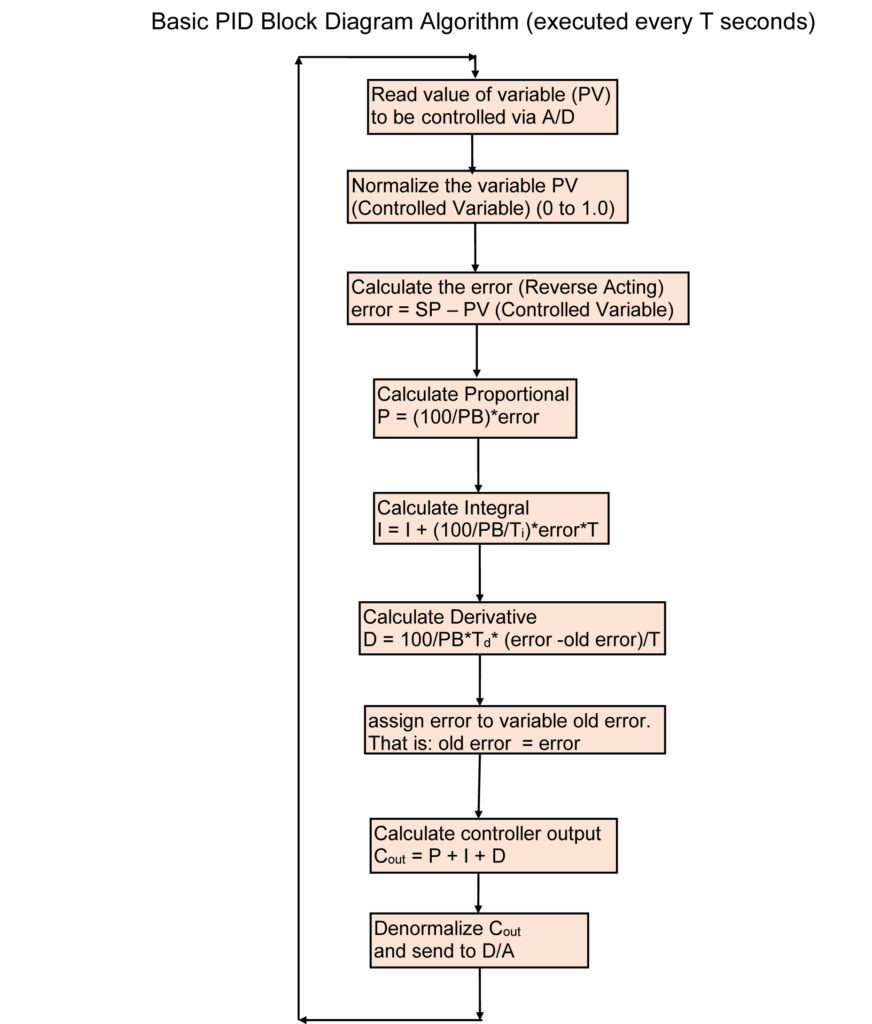
The diagram above illustrates the steps that occur in implementing a PID algorithm digitally. The first block and the final block are done outside of the PID function.
The following function declaration, part of the Compete Temperature C/C++ code, is used for filtering the Temperature Sensor.
float TR_C_filterFunction(float timeConstant, float processGain,float blockIn, float intervalTime);
The following function call is for the above filtering function.
TR_C_Filtered=TR_C_filterFunction(5, 1.0,TR_C, 1000); //filter time constant is first argument in seconds
The basic logic for a difference equation method 1st order filter is:
blockOut=blockOut +(intervalTime/1000/(timeConstant+intervalTime/1000))*(processGain*blockIn-blockOut);
ZNOL Autotune
This page will do the following:
- Explain the concept of Ziegler Nichols Open Loop (ZNOL) tuning concepts
- proportional, integral, and derivative
- Develop a graphical approach for generating the concepts
- Develop an approach for Automatically generating the Fast Autotune ZNOL contants
- Implement the approach on the Temperature Control System
- Describe the code and operation of the ZNOL Fast Autotuner
The graph below was captured from the Arduino Serial Plotter when running the program for the Temperature Control System. It was generated by creating a step change in the heater settings while the PID controller was in Manual mode. From a printout of the response, the appropriate geometry was applied manually. This included finding the inflection point and drawing a tanget whose intersection with the starting temperature yields the EffectivreDead Time. The 63.2% of the steady state value was found which enable finding the Time Constant . The Process gain was found by taking the ratio of the staedy state value of the Process Variable divided bt the change in heater setting. These three measurements were applied to the Ziegler Nichols formulas to yield the Proportional, Integral, and Derivative (PID) tuning constants.
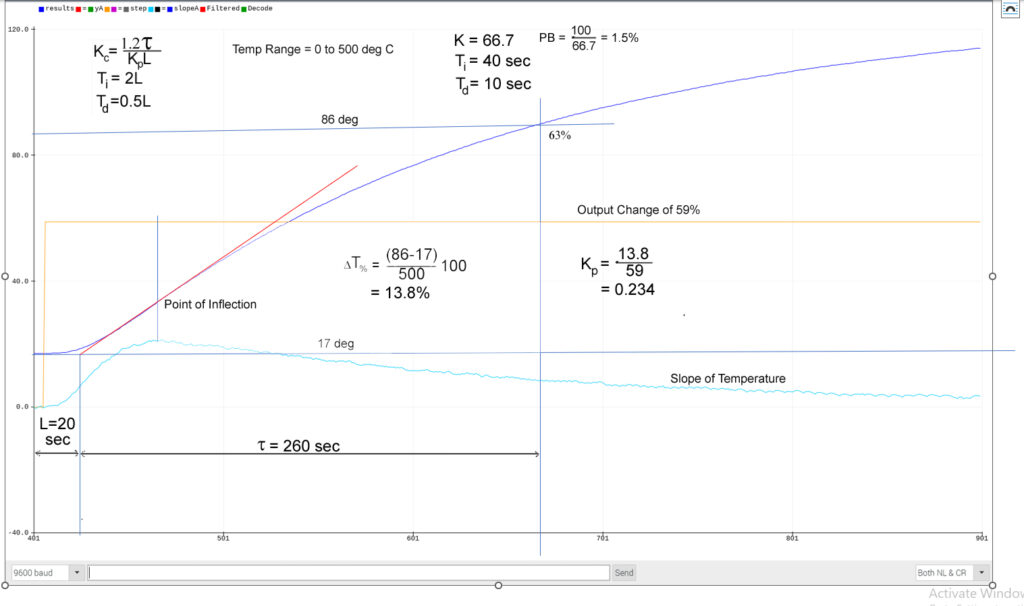
Autotuning will generate the proportional, integral, and derivative tuning constants and load them automatically into the PID controller. The approach is fast as the results are generated as soon as the point of inflection occurs, eliminating the need for the process to come to steady state.
The Autotune method for generating ZNOL tuning constants will be given in the link below:
Ziegler Nichols Open Loop Tuning Constants
The simplified code for generating the ZNOL Autotuning Constants is given in the link below:
Lab Experiments
Lab 4 – Autotune the Process that Uses LM35, the Sensor in the Middle of the Chamber.